Question

A triangular playground has sides that are lengths 2x feet, x-1 feet and x feet. If the perimeter of this playground is 27 feet, what are the

lengths of each side of the playground?

Answer 1

The lengths of the sides of the playground are 14 feet, 6 feet, 7 feet

Explanation:

At first, let us find the perimeter of the playground

∵ Perimeter of a triangle is P = S1 + S2 + S3

∵ The sides of the triangular playground are (2x) ft, (x - 1) ft, and x ft

∴ S1 = 2x, S2 = x - 1, S3 = x

→ Substitute them in the rule of the perimeter above

∵ P = 2x + x - 1 + x

→ Add the like terms

∴ P = (2x + x + x) - 1

∴ P = 4x - 1

∵ The perimeter of this playground is 27 feet

∴ P = 27

→ Equate the two values of P

∴ 4x - 1 = 27

→ Add 1 to both sides

∴ 4x - 1 + 1 = 27 + 1

∴ 4x = 28

→ Divide both sides by 4

∵
`(4x)/(4)` =
`(28)/(4)`

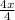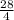
∴ x = 7

→ Substitute the value of x in each side to find their lengths

∵ S1 = 2(7)

∴ S1 = 14 feet

∵ S2 = 7 - 1

∴ S2 = 6 feet

∵ S3 = 7 feet

∴ The lengths of the sides of the playground are 14 feet, 6 feet, 7 feet