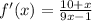Question

If it exists, solve for the inverse function of each of the following:

1. f(x) = 25x - 18
6. gala? +84 - 7
7. 10) = (b + 6) (6-2)
3. A(7)=-=-
4. f(x)=x
9. h(c) = V2c +2
+30
10. f(x) =
5. f(a) = a +8
ox-1
2. 9(x) = -1
2x+17
8. () - 2*​

Answer 1

The solution is too long. So, I included them in the explanation

Explanation:

This question has missing details. However, I've corrected each question before solving them

Required: Determine the inverse

1:

`f(x) = 25x - 18`

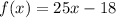
Replace f(x) with y

`y = 25x - 18`

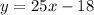
Swap y & x

`x = 25y - 18`

`x + 18 = 25y - 18 + 18`

`x + 18 = 25y`

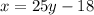
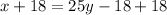
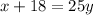
Divide through by 25

`(x + 18)/(25) = y`

`y = (x + 18)/(25)`

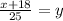
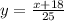
Replace y with f'(x)

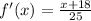
`f'(x) = (x + 18)/(25)`

2.
`g(x) = (12x - 1)/(7)`

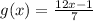
Replace g(x) with y

`y = (12x - 1)/(7)`

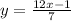
Swap y & x

`x = (12y - 1)/(7)`

`7x = 12y - 1`

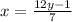
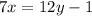
Add 1 to both sides

`7x +1 = 12y - 1 + 1`

`7x +1 = 12y`

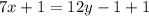
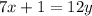
Make y the subject

`y = (7x + 1)/(12)`

`g'(x) = (7x + 1)/(12)`

3:
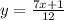
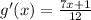
`h(x) = -(9x)/(4) - (1)/(3)`

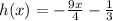
Replace h(x) with y

`y = -(9x)/(4) - (1)/(3)`

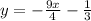
Swap y & x

`x = -(9y)/(4) - (1)/(3)`

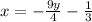
Add
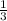`(1)/(3)` to both sides

`x + (1)/(3)= -(9y)/(4) - (1)/(3) + (1)/(3)`

`x + (1)/(3)= -(9y)/(4)`

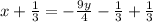
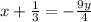
Multiply through by -4

`-4(x + (1)/(3))= -4(-(9y)/(4))`

`-4x - (4)/(3)= 9y`

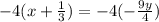
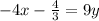
Divide through by 9

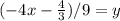
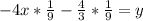
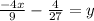
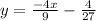
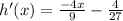
`(-4x - (4)/(3))/9= y`

`-4x * (1)/(9) - (4)/(3) * (1)/(9) = y`

`(-4x)/(9) - (4)/(27)= y`

`y = (-4x)/(9) - (4)/(27)`

`h'(x) = (-4x)/(9) - (4)/(27)`

4:

`f(x) = x^9`

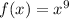
Replace f(x) with y

`y = x^9`

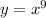
Swap y with x

`x = y^9`

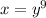
Take 9th root

`x^{(1)/(9)} = y`

`y = x^{(1)/(9)}`

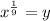
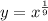
Replace y with f'(x)

`f'(x) = x^{(1)/(9)}`

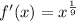
5:

`f(a) = a^3 + 8`

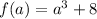
Replace f(a) with y

`y = a^3 + 8`

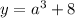
Swap a with y

`a = y^3 + 8`

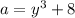
Subtract 8

`a - 8 = y^3 + 8 - 8`

`a - 8 = y^3`

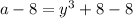
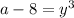
Take cube root

`\sqrt[3]{a-8} = y`

`y = \sqrt[3]{a-8}`

Replace y with f'(a)

`f'(a) = \sqrt[3]{a-8}`

6:

`g(a) = a^2 + 8a- 7`

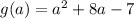
Replace g(a) with y

`y = a^2 + 8a - 7`

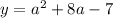
Swap positions of y and a

`a = y^2 + 8y - 7`

`y^2 + 8y - 7 - a = 0`

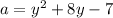
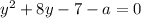
Solve using quadratic formula:

`y = (-b\±√(b^2 - 4ac))/(2a)`

`a = 1` ;
`b = 8`;
`c = -7 - a`

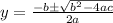
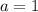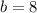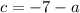
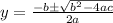`y = (-b\±√(b^2 - 4ac))/(2a)` becomes

`y = (-8 \±√(8^2 - 4 * 1 * (-7-a)))/(2 * 1)`

`y = (-8 \±√(64 + 28 + 4a))/(2 * 1)`

`y = (-8 \±√(92 + 4a))/(2 * 1)`

`y = (-8 \±√(92 + 4a))/(2 )`

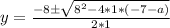
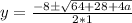
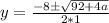
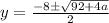
Factorize

`y = (-8 \±√(4(23 + a)))/(2 )`

`y = (-8 \±2√((23 + a)))/(2 )`

`y = -4 \±√((23 + a))`

`g'(a) = -4 \±√((23 + a))`

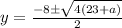
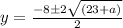
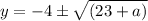
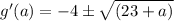
7:

`f(b) = (b + 6)(b - 2)`

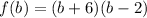
Replace f(b) with y

`y = (b + 6)(b - 2)`

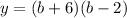
Swap y and b

`b = (y + 6)(y - 2)`

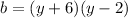
Open Brackets

`b = y^2 + 6y - 2y - 12`

`b = y^2 + 4y - 12`

`y^2 + 4y - 12 - b = 0`

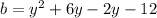
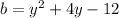
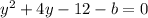
Solve using quadratic formula:

`y = (-b\±√(b^2 - 4ac))/(2a)`

`a = 1` ;
`b = 4`;
`c = -12 - b`

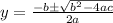
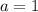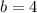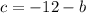
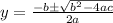`y = (-b\±√(b^2 - 4ac))/(2a)` becomes

`y = (-4\±√(4^2 - 4 * 1 * (-12-b)))/(2*1)`

`y = (-4\±√(4^2 - 4 *(-12-b)))/(2)`

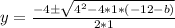
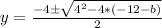
Factorize:

`y = (-4\±√(4(4 - (-12-b))))/(2)`

`y = (-4\±2√((4 - (-12-b))))/(2)`

`y = (-4\±2√((4 +12+b)))/(2)`

`y = (-4\±2√(16+b))/(2)`

`y = -2\±√(16+b)`

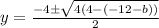
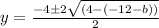
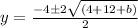
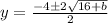
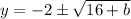
Replace y with f'(b)

`f'(b) = -2\±√(16+b)`

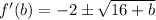
8:

`h(x) = (2x+17)/(3x+1)`

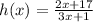
Replace h(x) with y

`y = (2x+17)/(3x+1)`

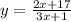
Swap x and y

`x = (2y+17)/(3y+1)`

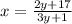
Cross Multiply

`(3y + 1)x = 2y + 17`

`3yx + x = 2y + 17`

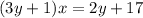
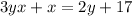
Subtract x from both sides:

`3yx + x -x= 2y + 17-x`

`3yx = 2y + 17-x`

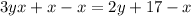
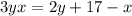
Subtract 2y from both sides

`3yx-2y =17-x`

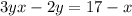
Factorize:

`y(3x-2) =17-x`

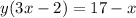
Make y the subject

`y = (17 - x)/(3x - 2)`

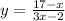
Replace y with h'(x)

`h'(x) = (17 - x)/(3x - 2)`

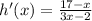
9:

`h(c) = √(2c + 2)`

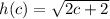
Replace h(c) with y

`y = √(2c + 2)`

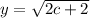
Swap positions of y and c

`c = √(2y + 2)`

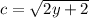
Square both sides

`c^2 = 2y + 2`

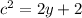
Subtract 2 from both sides

`c^2 - 2= 2y`

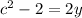
Make y the subject

`y = (c^2 - 2)/(2)`

`h'(c) = (c^2 - 2)/(2)`

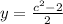
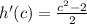
10:

`f(x) = (x + 10)/(9x - 1)`

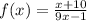
Replace f(x) with y

`y = (x + 10)/(9x - 1)`

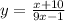
Swap positions of x and y

`x = (y + 10)/(9y - 1)`

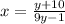
Cross Multiply

`x(9y - 1) = y + 10`

`9xy - x = y + 10`

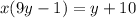
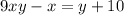
Subtract y from both sides

`9xy - y - x = y - y+ 10`

`9xy - y - x = 10`

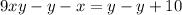
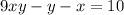
Add x to both sides

`9xy - y - x + x= 10 + x`

`9xy - y = 10 + x`

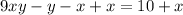
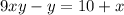
Factorize

`y(9x - 1) = 10 + x`

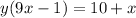
Make y the subject

`y = (10 + x)/(9x - 1)`

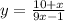
Replace y with f'(x)

`f'(x) = (10 + x)/(9x -1)`