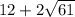Answer:
Perimeter of ∆ABR =
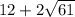
Explanation:
Given, A(-2, -1), B(10, -1), and R(4, 4).
Perimeter of ∆ABR =
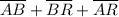
Distance between A(-2, -1) and B(10, -1) using distance formula:
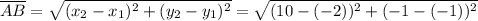
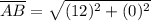
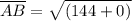
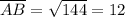
Distance between B(10, -1) and R(4, 4):
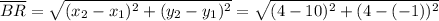
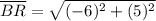
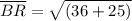
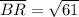
Distance between A(-2, -1) and R(4, 4):
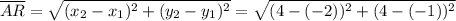
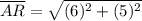
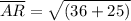
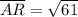
Perimeter of ∆ABR =
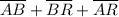
Perimeter of ∆ABR =
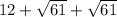
Perimeter of ∆ABR =