Question

A frustum is formed when a plane parallel to a cone’s base cuts off the upper portion as shown.

A cone is shown. The top of the cone is cut off to form a frustum of the bottom portion. The cone has a radius of 3.5 and a height of 8. The frustum has a height of 11 and a radius of 7.5.

Which expression represents the volume, in cubic units, of the frustum?

One-thirdπ(7.52)(11) – One-thirdπ(3.52)(8)
One-thirdπ(7.52)(11) + One-thirdπ(3.52)(8)
One-thirdπ(7.52)(19) – One-thirdπ(3.52)(8)
One-thirdπ(7.52)(19) + One-thirdπ(3.52)(8)

Answer 1

The volume of the frustum can be found using the formula for the volume of a frustum of a cone, which is given by:
`Volume = (1/3)πh(r1² + r1r2 + r2²).`

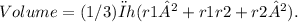
Step-by-step explanation:

The volume of the frustum can be found using the formula for the volume of a frustum of a cone, which is given by:

`Volume = (1/3)πh(r1² + r1r2 + r2²)`

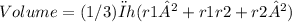
Where h is the height of the frustum, r1 is the radius of the smaller base of the frustum, and r2 is the radius of the larger base of the frustum.

Substituting the given values, we have:

`Volume = (1/3)π(11)(3.5² + 3.5(7.5) + 7.5²)`

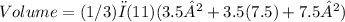
simplifying this expression will give you the correct volume of the frustum.

Answer 2

I think the answer looks B