Final answer:
The volume of the frustum can be found using the formula for the volume of a frustum of a cone, which is given by:

Step-by-step explanation:
The volume of the frustum can be found using the formula for the volume of a frustum of a cone, which is given by:
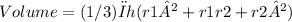
Where h is the height of the frustum, r1 is the radius of the smaller base of the frustum, and r2 is the radius of the larger base of the frustum.
Substituting the given values, we have:
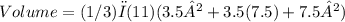
simplifying this expression will give you the correct volume of the frustum.