Question

The time (in number of days) until maturity of a certain variety of tomato plant is Normally distributed with mean μ. You select a simple random sample of four plants of this variety and measure the time until maturity. The four times, in days, are as follows: 63 69 62 66 with standard deviation 3.16.

Required:
Calculate the 99% confidence interval for population mean μ. Find the closest answer

Answer 1

Answer: 60.93 < μ < 69.07

Explanation: The true mean of a set of data is between an interval of values with a percentage of precision, e.g., a 99% confidence interval means we are 99% confident the true mean is between the lower and upper limits.

To find the interval, use

x±
`z(s)/(√(n))`

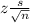
z is z-score related to the % of confidence level

In this case, a 99% confidence interval is 2.576

x is sample mean

Calculating:

`x=(63+69+62+66)/(4)`

x = 65

65±
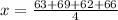
`2.576(3.16)/(√(4))`

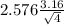
65±4.07

Confidence Interval: 60.93 < μ < 69.07

Meaning that we are 99% sure the population means is between 60.93 and 69.07.