Question

A particular fruitâs weights are normally distributed, with a mean of 598 grams and a standard deviation of 6 grams. The heaviest 8% of fruits weigh more than how many grams? Give your answer to the nearest gram.

Answer 1

The 8% of the fruit weigh more than
`x=606.43 \ g`

Explanation:

From the question we are told that

The mean is
`\mu = 598 \ g`

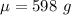
The standard deviation is
`\sigma = 6 \ g`

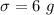
Generally the 8% is mathematically represented as

`P(X > x) = 0.08`

=>
`P(X > x) = P ( (X - \mu)/(\sigma )>(x - 598)/(6) )=0.08`

`(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )`

`P(X > x) = P ( Z >(x - 598)/(6) )=0.08`

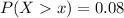
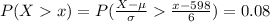
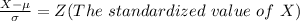
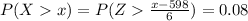
From the normal distribution table the critical value corresponding area representing 0.08 towards the right tail of the curve is

`z = 1.405`

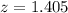
So

`(x- 598)/(6) = 1.405`

=>
`x=606.43 \ g`