Answer:
a
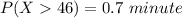
b

Explanation:
From the question we are told that
The procedure for performing a certain task is uniformly distributed on the interval from( a = 32 )minutes to (b= 52) minutes
Generally the cumulative distribution function for continuous uniform distribution is
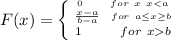
Generally the probability that it takes more than 46 minutes to learn the procedure is mathematically represented as
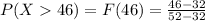
=>
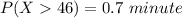
Generally the average time required to learn the procedure is mathematically represented as
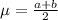
=>

=>
