Answer:
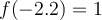
Explanation:
Given function:
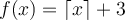
This is a Ceiling Function, denoted by the square brackets [ ] with the bottom part missing.
When graphing a Ceiling Function:
- open dot means "not including"
- solid dot means "including"
The Ceiling Function gives us the nearest integer up.
So the ceiling of x = -2.2 is -2, as the greatest integer that is more than (or equal to) -2.2 is -2
Therefore:
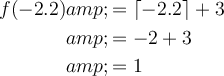
This is confirmed when using the graph to solve.
To find f(-2.2), locate x = -2.2 on the graph.
Trace up vertically until a step is reached.
The step in this part is not including -3 and including -2, so this confirms that x = -2.2 is in this interval.
Trace along horizontally to the y-axis to find the corresponding y-value, which is 1.
Therefore, f(-2.2) = 1