Question

Heights were measured for a random sample of 10 plants grown while being treated with a particular nutrient. The sample mean and sample standard deviation of those height measurements were 46 centimeters and 7 centimeters, respectively. Assume that the population of heights of treated plants is normally distributed with mean μ. Based on the sample, can it be concluded that μ is different from 45 centimeters? Use the 0.05 level of significance.

Answer 1

The calculated value t = 0.452< 2.2621 at 0.05 level of significance

null hypothesis is accepted

Based on the sample, can it be concluded that μ is not different from 45 centimeters

Explanation:

Step( i ):-

Heights were measured for a random sample of 10 plants

Size of the sample 'n' = 10

Mean of the sample (x⁻ ) = 46 centimeters

Standard deviation of the sample (s) = 7 centimeters

Mean of the Population ( μ ) = 45

Step(ii):-

Null Hypothesis :H₀:( μ ) = 45

Alternative Hypothesis : H₁: μ ) ≠ 45

Test statistic

`t = (x^(-)-mean )/((S)/(√(n) ) )`

`t = (46-45)/((7)/(√(10) ) )`

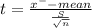
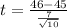
t = 0.452

Degrees of freedom

γ = n-1 = 10 -1 = 9

t₀.₀₅ = 2.2621

The calculated value t = 0.452< 2.2621 at 0.05 level of significance

null hypothesis is accepted

Based on the sample, can it be concluded that μ is not different from 45 centimeters