Answer: 0.9972
Explanation:
Let x be a random variable that represents the strength of concrete cylinders.
Given: The compressive strengths of 40 concrete cylinders have an estimated mean
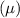 of 60.14 MPa and standard deviation
of 60.14 MPa and standard deviation
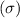 of 5.02 MPa.
of 5.02 MPa.
The probability that 10 cylinders will each have strengths between 45 and 75 MPa :
![P(45<\overline{x}<75)=P((45-60.14)/(5.02)<\frac{\overline{x}-\mu}{\sigma}<(75-60.14)/(5.02))\\\=P(-3.016<z<2.96)\\\\=P(z<2.96)-P(z<-3.016)\\\\=P(z<2.96)-(1-P(z<3.016))\\\\=0.9985-(1-0.9987)\ \ \ [\text{by p-value table}]\\\\= 0.9972](https://img.qammunity.org/2021/formulas/mathematics/college/yv6ha4ftfupxhobx2atu395iq0dq8zqhoj.png)
Hence, The required probability = 0.9972