Question

Jimmy purchased 15 tickets to a concert and spent $140. He purchased some children's tickets and some adult tickets. The children's tickets cost $7 each and the adult tickets cost $12 each. Write a system that represents this situation. How many of each did Jimmy purchase?​

Answer 1

Jimmy purchased 8 of the children's ticket and 7 of the adult's ticket.

Explanation:

Let c = children tickets

Let a = adult tickets

Given the following data;

Number of tickets = 15

Total amount spent = $140

Cost of each children ticket = $7

Cost of each adult ticket = $12

*Translating the word problem into an algebraic equation (system)*

For the total number of tickets;

`c + a = 15` .........equation 1

For the total amount spent;

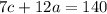`7c + 12a = 140` ..........equation 2

*Solving the linear equation by using the substitution method*

Making c the subject in equation 1:

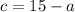`c = 15 - a` .......equation 3

Substituting "c" into equation 2;

`7(15 - a) + 12a = 140`

Simplifying the equation, we have;

`105 - 7a +12a = 140`

`105 + 5a = 140`

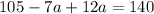
Rearranging the equation, we have;

`5a = 140 - 105`

`5a = 35`

`a = \frac {35}{5}`

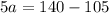
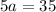
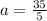
a = 5 (For the $12 adult ticket).

To find the number of children tickets;

Substituting "a" into equation 3;

`c = 15 - 7`

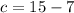
c = 8 (For the $7 children ticket).