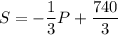Question

A charter airline finds that on its Saturday flights from Philadelphia to London all 180 seats will be sold if the ticket price is $200. However, for each $3 increase in ticket price, the number of seats sold decreases by one. (a) Find a formula for the number of seats sold S if the ticket price is P dollars.

Answer 1

`S = -(1)/(3)P+(740)/(3)`

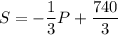
Explanation:

Given that:

Number of seats sold is 180 with ticket price $200.

Number of seats decreases by one when the ticket price is increased by $3.

To find:

The formula for the number of seats sold (S) when the ticket price is P dollars.

Solution:

It is linear dependency of number of seats sold, S on ticket price, P.

`S\propto P`

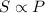
It can be written as:

`S = kP+C`

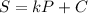
Where
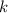`k` is the constant of proportionality and

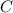`C` is a constant.

Now, putting the given values:

`180 = 200k +C ..... (1)`

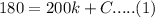
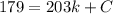`179 = 203k+C` ...... (2)

Subtracting (1) from (2):

`3k = -1\\\Rightarrow k =-(1)/(3)`

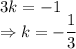
Putting the value in (1):

`\Rightarrow C = 180+(200)/(3) = (740)/(3)`

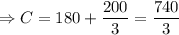
Therefore the equation becomes:

`S = -(1)/(3)P+(740)/(3)`