Question

5. Justify the last two steps of the proof.

(4 points)

Given: RS UT and RT US

Prove: ARST AUTS

T

0

Proof:

1. RSU

2. RT & US

3. ST & TS

4. ARST AUTS

1. Given

2. Given

3. ?

4. ?

E

Answer 1

Your question isn't 100% clear to me but I did my best:

1. RS = UT Given

2. RT = US Given

3. ST = TS Reflexive Property of Congruence

4. RST = UTS SSS (Side-Side-Side)

Answer 2

ST & TS are congruent

RST and UTS are congruent

Explanation:

The question is not properly presented; however, I've added an attachment to give a clear picture of the question.

Required

State the property that justifies:

`ST = TS`

Triangles
`RST = UTS`

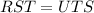
From the question, we have that:

`RS = UT`

`RT = US`

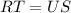
In plane geometry, the length of ST is still the same as the length of TS.

This implies that:

`ST = TS` because ST is congruent to TS

Moving further to determine the relationship between triangles
`RST\ \&\ UTS`

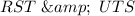
Comparing both triangles:

They have a similar side ST and TS because
`ST = TS`

And we also have that:
`RS = UT`

So, we can conclude that:
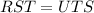`RST = UTS` because they are congruent