Question

A sample of 12001200 computer chips revealed that 53S% of the chips do not fail in the first 10001000 hours of their use. The company's promotional literature claimed that more than 50P% do not fail in the first 10001000 hours of their use. Is there sufficient evidence at the 0.100.10 level to support the company's claim

Answer 1

Complete Question

A sample of 1200 computer chips revealed that 53% of the chips do not fail in the first 1000 hours of their use. The company's promotional literature claimed that more than 50% do not fail in the first 1000 hours of their use. Is there sufficient evidence at the 0.10 level to support the company's claim

Answer:

The decision rule is

Reject the null hypothesis

The conclusion is

There is sufficient evidence to conclude that the company's promotional literature claimed that more than 50% do not fail in the first 1000 hours of their use is correct

Explanation:

From the question we told that

The sample size is n = 1200

The significance level is
`\alpha = 0.100`

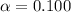
The sample proportion is
`\^ p = 0.53`

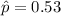
The null hypothesis
`H_o : p = 0.50`

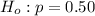
The alternative hypothesis is
`Ha : p > 0.50`

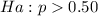
Generally the test statistics is mathematically represented as

`z = \frac{\^ p - p }{ \sqrt{(p(1 - p ))/(n) } }`

=>
`z = \frac{ 0.53 - 0.5 }{ \sqrt{(0.50 (1 - 0.50))/(1200) } }`

=>
`z = 2.078`

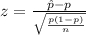
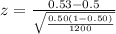
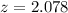
From the z table the area under the normal curve to the right corresponding to 2.078 is

`P(Z > 2.078 ) = 0.018855`

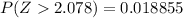
So

`p-value = 0.018855`

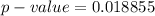
Generally the value obtained we see that
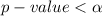`p-value < \alpha` , Hence

The decision rule is

Reject the null hypothesis

The conclusion is

There is sufficient evidence to conclude that the company's promotional literature claimed that more than 50% do not fail in the first 1000 hours of their use is correct