Answer:
The tangential speed at Livermore is approximately 284.001 meters per second.
Step-by-step explanation:
Let suppose that the Earth rotates at constant speed, the tangential speed (
 ), measured in meters per second, at Livermore (37.6819º N, 121º W) is determined by the following expression:
), measured in meters per second, at Livermore (37.6819º N, 121º W) is determined by the following expression:
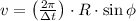 (1)
(1)
Where:
 - Rotation time, measured in seconds.
- Rotation time, measured in seconds.
 - Radius of the Earth, measured in meters.
- Radius of the Earth, measured in meters.
 - Latitude of the city above the Equator, measured in sexagesimal degrees.
- Latitude of the city above the Equator, measured in sexagesimal degrees.
If we know that
 ,
,
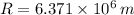 and
and
 , then the tangential speed at Livermore is:
, then the tangential speed at Livermore is:
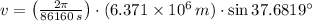
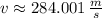
The tangential speed at Livermore is approximately 284.001 meters per second.