Answer:
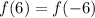 --- True
--- True
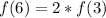 --- False
--- False
Explanation:
Given
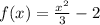
Solving (a): f(6) = f(-6)
First, we solve for f(6) by substituting 6 for x in
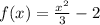
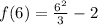
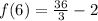
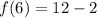

Next, we solve for f(-6) by substituting -6 for x in
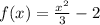
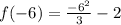
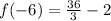
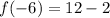
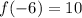
We have that:

Hence, the statement is true
Solving (b):
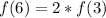
We have that:

Next, we solve for f(3) by substituting 3 for x in
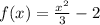
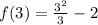
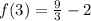
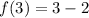
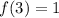
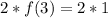
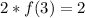
So:
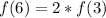
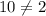
Hence, the statement is false