Answer:
The potential is

Step-by-step explanation:
From the question we are told that
The magnitude of the charge is
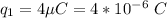
The position of the charge is

The magnitude of the second charge is
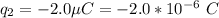
The position is
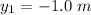
The position of point A is

Generally the electric potential at A due to the first charge is mathematically represented as
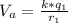
Here k is the coulombs constant with value
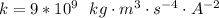
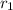 is the distance between first charge and a which is mathematically represented as
is the distance between first charge and a which is mathematically represented as

=>
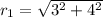
=>
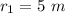
So


Generally the electric potential at A due to the second charge is mathematically represented as
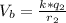
Here k is the coulombs constant with value
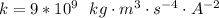
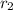 is the distance between second charge and a which is mathematically represented as
is the distance between second charge and a which is mathematically represented as
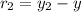
=>
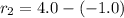
=>
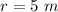
So
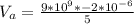
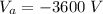
So the net potential difference at point A due to the charges is mathematically represented as
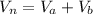
=>
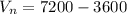
=>

Generally the net potential difference at the origin due to both charges is mathematically represented as
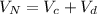
Here
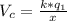
=>
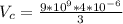
=>

and
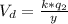
=>
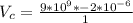
=>
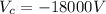
Generally the net potential difference at the origin is

=>

Generally the potential difference at A relative to zero at the origin is mathematically evaluated as
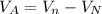
=>

=>
