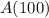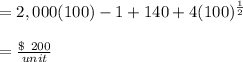Question

If C(x) is the cost of producing x units of a commodity, then the average cost per unit is c(x) = C(x)/x. Consider the cost function C(x) given below. C(x) = 16,000 + 140x + 4x3/2 (a) Find the total cost at a production level of 1000 units. (Round your answer to the nearest cent.)(b) Find the average cost at a production level of 1000 units. (Round your answer to the nearest cent.) (c) Find the marginal cost at a production level of 1000 units. (Round your answer to the nearest cent.)(d) Find the production level that will minimize the average cost. (Round your answer to the nearest whole number.) (e) What is the minimum average cost? (Round your answer to the nearest dollar.)

Answer 1

Following are the solution to the question:

Step-by-step explanation:

Calculating the total cost:

`C(x) = 2,000 + 140x + (4x^3)/(2)`

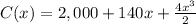
Calculating the marginal cost:

`M(x) = C'(x) = 140 + 6 * (1)/(2)`

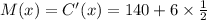
Calculating the average cost:

`A( x ) =( C( x ))/(x) = 2,000x-1 + 140 + 4* (1)/(2)`

Calculating the marginal average cost:

`m( x ) = A'( x ) = -2,000x-2 + 2x-(1)/(2)`

In point (a)

`C( 1,000 )`

`= 2,000 + 140( 1,000 ) + 4( 1,000)^{(3)/(2)}\\\\= \$ \ 268,491.106 \\\\ = \$ \ 268,491.11`

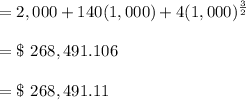
In point(b)

`A( 1,000 )`

`= 2,000( 1,000 )-1 + 140 + 4( 1,000 )^{(1 )/(2)}\\\\= \frac{\$ \ 268.491106} {unit}\\\\= (\$ \ 268.49)/( unit)`

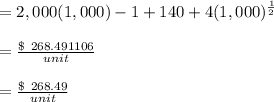
In point (c)

`M( 1,000)`

`= 140 + 6( 1,000 )^{(1)/(2)}\\\\= (\$ \ 329.73666)/(unit)\\\\= ( \$ \ 329.74)/( unit)`

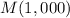
In point (d)

Calculating the average cost:

`A'( x ) = m( x ) = -2,000x-2 + 2x- (1)/(2)\\\\A'( x ) = 0 = -2,000x-2 + 2x-(1)/(2)= 0\\\\multiply \ by \ 2\\\\\to -2,000 + 2 * (x^3)/(2)= 0 \\\\\to 2* (x^3)/(2) = 2,000 \\\\\to (x^3)/(2) = (2,000)/(2) \\\\ \to (x^3)/(2)= 1,000 \\\\\to x = ( 1,000 )^{(2)/(3)}\\\\ \to 100 \ units`

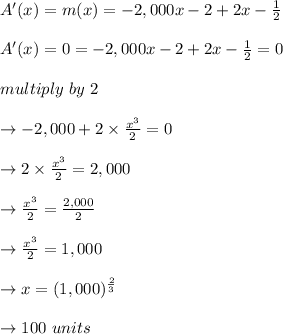
In point (e)

`A( 100 )`

`= 2,000( 100 )-1 + 140 + 4( 100 )^{(1)/(2)}\\\\= ( \$ \ 200)/(unit)`