Question

A person swings a 0.546-kg tether ball tied to a 4.56-m rope in an approximately horizontal circle. If the maximum tension the rope can withstand before breaking is 11.0 N, what is the maximum angular speed of the ball

Answer 1

2.1 rad/s

Step-by-step explanation:

Given that,

Mass of a tether ball, m = 0.546 kg

Length of a rope, l = 4.56 m

The maximum tension the rope can withstand before breaking is 11.0 N

We need to find the maximum angular speed of the ball. Let v is the linear velocity. The maximum tension is balanced by the centripetal force acting on it. It can be given by :

`F=(mv^2)/(r)\\\\v=\sqrt{(Fr)/(m)} \\\\v=\sqrt{(11* 4.56)/(0.546)} \\\\=9.584\ m/s`

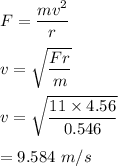
Let
`\omega` is the angular speed of the ball. The relation between the angular speed and angular velocity is given by :

`v=r\omega\\\\\omega=(v)/(r)\\\\=(9.584)/(4.56)\\\\=2.1\ rad/s`

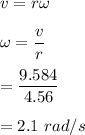
So, the maximum angular speed of the ball is 2.1 rad/s.