Question

Jane has 34 candles leftover from the last craft show and Brianna

has 2 candles. They are making more candles for the next show.

Jane makes 24 candles per hour and Brianna makes 32 candles per

hour. They are also going to use the candles left over from the last

show and want to have the same number of candles at their stalls for

this show. Let h represent the number of hours they need to work

for this.

Answer 1

4 hours

Explanation:

Given that the number of leftover candles for Jane = 34

and the number of leftover candles for Brianna = 2

Rate of candle making for Jane = 24 candles/ hour

Rate of candle making for Jane = 32 candles/ hour

As they work for h hours to make candles.

So, in h hours, the number of new candles made by Jane = 24h candles

For Jane, the total number of candles after h houres, including the leftover candles
`= 24h+34 \cdots(i)`

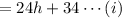
Similarly, in h hours, the number of new candles made by Brianna = 32h candles

For Brianna, the total number of candles after h houres, including the leftover candles
`= 32h+2 \cdots(ii).`

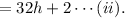
As they want to have the same number of candles at their stalls, so equating the numbers of candles from equations (i) and (ii), we have

`24h+34=32h+2 \\\\\Rightarrow 32h-24h=34-2 \\\\\Rightarrow 8h=32\\\\`

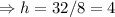`\Rightarrow h=32/8=4` hours.

Hence, both need to work for 4 hours to have the same number of candles.