Question

An airplane is preparing to land at an airport. It is 44,8000 feet above the ground and is descending at the rate of 3,100 feet per minute. At the same​ airport, another airplane is taking off and will ascend at the rate of 2,500 feet per minute. When will the two airplanes be at the same altitude and what will that altitude​ be? Use two other methods to solve the problem. Explain which methods are easier to use and which are more difficult to use for the situation.

Answer 1

Time: 8 minutes

Altitude: 20000ft

Method 1 is easiest

Method 3 is easiest

Explanation:

Given

Airplane 1:

`Height = 44800 ft`

`Descending\ Rate = 3100ft/min`

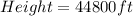
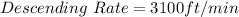
Airplane 2:

`Ascending\ Rate = 2500ft/min`

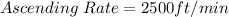
Required

Determine when both planes would be at the same altitude?

Let the minute be represented by m

For Airplane 1, Its altitude at any height h is:

`Airplane\ 1 = Height - Descending\ Rate * m`

It is minus (-) because the airplane is descending

`Airplane\ 1 = 44800 - 3100 * m`

`Airplane\ 1 = 44800 - 3100m`

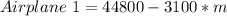
For Airplane 2, Its altitude at any height h is:

`Airplane\ 2 = Ascending\ Rate * m`

`Airplane\ 2 = 2500 * m`

`Airplane\ 2 = 2500m`

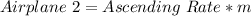
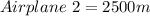
Method 1:

For both heights to be equal, we have that:

`Airplane\ 1 = Airplane\ 2`

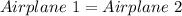
This gives:

`44800 - 3100m = 2500m`

Collect Like Terms

`44800 = 2500m + 3100m`

`44800 = 5600m`

`5600m = 44800`

`m = 44800/5600`

`m = 8\ min`

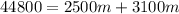
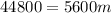
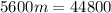
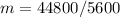
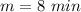
Hence, the time they will be at the same altitude is 8 minutes

Substitute 8 for m in

`Airplane\ 2 = 2500m`

`Airplane\ 2 = 2500 * 8`

`Airplane\ 2 = 20000\ ft`

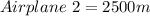
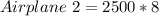
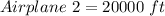
Hence, they will be at the same altitude at 20000ft

Method 2:

We have that:

`Airplane\ 1 = 44800 - 3100m`

`Airplane\ 2 = 2500m`

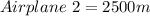
Since they are to be at the same altitude, then

The difference in their altitude must be 0

i.e.

`Airplane\ 1 - Airplane\ 2 = 0`

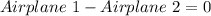
This gives

`44800 - 3100m - 2500m = 0`

`44800 - 5600m = 0`

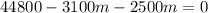
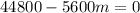
Collect Like Terms

`5600m = 44800`

`m = 44800/5600`

`m = 8\ min`

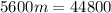
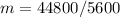
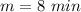
Substitute 8 for m in

`Airplane\ 1 = 44800 - 3100m`

`Airplane\ 1 = 44800 - 3100 * 8`

`Airplane\ 1 = 44800 - 24800`

`Airplane\ 1 = 20000\ ft`

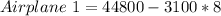
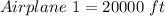
Method 3:

We have that:

`Airplane\ 1 = 44800 - 3100m`

`Airplane\ 2 = 2500m`

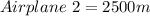
Since they are to be at the same altitude, then

The ratio of their altitudes must be 1

i.e.

`(Airplane\ 1)/(Airplane\ 2) = 1`

`(44800 - 3100m)/(2500m) = 1`

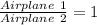
Cross Multiply

`44800 - 3100m = 1 * 2500m`

`44800 - 3100m = 2500m`

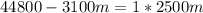
Collect Like Terms

`44800 = 2500m + 3100m`

`44800 = 5600m`

`5600m = 44800`

`m = 44800/5600`

`m = 8\ min`

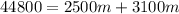
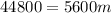
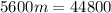
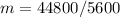
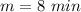
Substitute 8 for m in

`Airplane\ 1 = 44800 - 3100m`

`Airplane\ 1 = 44800 - 3100 * 8`

`Airplane\ 1 = 44800 - 24800`

`Airplane\ 1 = 20000\ ft`

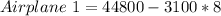
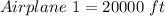
Hence;

Their altitudes must be 20000ft

Though the three methods applied uses the same logic at some point, the first method applied is still the easiest and it is a straight forward method that could be applied in solving the question.

Method 3 is the most difficult.