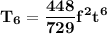Question

Find the 7th term in the following binomial expansion(4f+t/3)8 in ascending powers of t

Answer 1

`\displaystyle T_6=(448)/(729) f^2t^6`

Explanation:

Binomial Theorem

Any power of x + y can be expanded into a sum of the form:

`\displaystyle (x+y)^(n)={n \choose 0}x^(n)y^(0)+{n \choose 1}x^(n-1)y^(1)+{n \choose 2}x^(n-2)y^(2)+\cdots +{n \choose n-1}x^(1)y^(n-1)+{n \choose n}x^(0)y^(n)`

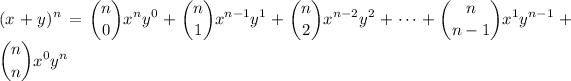
For any given term k, counted from 0 to n:

`\displaystyle T_k={n \choose k}x^(n-k)y^(k)`

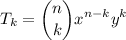
Note if we have to find the 7th term, we have to use k=6. The expression is:

`\displaystyle \left(4f+(t)/(3)\right)^8`

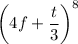
For n=8, x=4f, y=t/3, k=6:

`\displaystyle T_6={8 \choose 6}(4f)^(8-6)\left ((t)/(3) \right )^(6)`

`\displaystyle T_6={8 \choose 6}(4f)^(2)\left ((t)/(3) \right )^(6)`

`\displaystyle T_6={8 \choose 6}16f^2(t^6)/(3^6)`

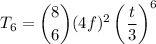
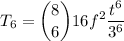
Calculate:

`\displaystyle {8 \choose 6}=(8!)/(2!\cdot 6!)=28`

Thus:

`\displaystyle T_6=28\cdot 16f^2(t^6)/(729)`

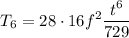
Simplifying, the 7th term is:

`\mathbf{\displaystyle T_6=(448)/(729) f^2t^6}`