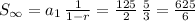Question

The fourth term of a geometric progression is 4 and the seventh term is 32/125. Find the first term, the common ratio and the sum of the first nth terms. Hence, deduce the sum to infinity.​

Answer 1

common ratio is 2/5

First term is 125/2

The sum of the first n terms is:
`S_n=(125)/(2) \, (1-(2/5)^n)/(3/5)`

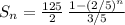
The infinite sum is:
`S_\infty =(625)/(6)`

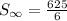
Explanation:

The 4th term is 4, and the seventh term is 32/125 so we use the definition of nth term of a geometric sequence to create the following two equations:

`a_4=a_1\,*\,r^(4-1) = a_1\,*\,r^3\\4=a_1\,*\,r^3\\and\\a_7=a_1\,*\,r^(7-1) = a_1\,*\,r^6\\(32)/(125) = a_1\,*\,r^6`

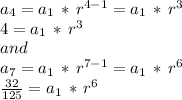
Now we divide a7 by a4 to get rid of a1 and work on determining the common ratio of the sequence:

`(a_7)/(a_4) =(8)/(125) =(a_1\,r^6)/(a_1\,r^3) =r^3\\then\\r=\sqrt[3]{(8)/(125) } =(2)/(5)`

So, the common ratio is 2/5

we can now determine the first term:

`a_4=4=a_1\,*\,(2/5)^3\\a_1=(125*4)/(8) =(125)/(2)`

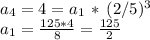
The sum of the first n terms is given by the formula:

`S_n=(125)/(2) \, (1-(2/5)^n)/(1-(2/5)) \\S_n=(125)/(2) \, (1-(2/5)^n)/(3/5)`

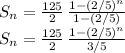
and therefore, the infinite sum is:

`S_\infty = a_1\,(1)/(1-r) = (125)/(2) \,(5)/(3) =(625)/(6)`