Line A goes through points (-2,3) and (-1,1). Line B goes through points (0,-3) and (2,-2). Fill in the blank: Lines A and B are ______.

Question

asked Oct 24, 2021 148k views

2 Answers

Fernando Aspiazu · Answer 1 · 2021-10-29T14:14:10+0000

Answer:

Lines A and B are perpendicular.

Explanation:

Line A goes through points (-2,3) and (-1,1).

Finding the slope of line A

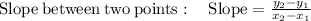
$\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

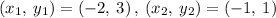
$\left(x_1,\:y_1\right)=\left(-2,\:3\right),\:\left(x_2,\:y_2\right)=\left(-1,\:1\right)$

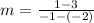
$m=(1-3)/(-1-\left(-2\right))$

m=-2

Line B goes through points (0,-3) and (2,-2).

Finding the slope of line B

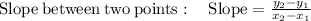
$\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

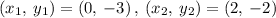
$\left(x_1,\:y_1\right)=\left(0,\:-3\right),\:\left(x_2,\:y_2\right)=\left(2,\:-2\right)$

$m=(-2-\left(-3\right))/(2-0)$

m=(1)/(2)

Please note that the slope of line A is a negative reciprocal of line B and vice versa.

As we know that the slopes of two perpendicular lines are negative reciprocals of each other.

Therefore, lines A and B are perpendicular.