Question

Select the equation that represents the line that passes through (1,7) and is parallel to y = 5x + 4

Answer 1

a

Explanation:

it has to have to same slope as the first equation so you have y=5x+b then what you do is plug in the points and solve for b. which gives you 2. so your final equation is y=5x+2

7=5+b

-5 -5

2=b

Answer 2

The equation that represents the line that passes through (1,7) and is parallel to y = 5x + 4 will be:

• 
  `y=5x+2`

Explanation:

Given the equation

`y = 5x + 4`

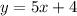
Here the slope is:

`m=5`

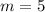
as comparing with the
`y=mx+b`, which is the slop-intercept form where m is the slope and b is the y-intercept.

As we know the point-slope form is

`y-y_1=m\:\left(x-x_1\right)`

`y-7=5\left(x-1\right)`

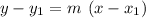
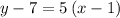
Add 7 to both sides

`y-7+7=5\left(x-1\right)+7`

`y=5x+2`

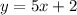
Therefore, the equation that represents the line that passes through (1,7) and is parallel to y = 5x + 4 will be:

• 
  `y=5x+2`