Question

How would I do the steps to solve this?

Answer 1

The maximum revenue is 16000 dollars (at p = 40)

Explanation:

One way to find the maximum value is derivatives. The first derivative is used to find where the slope of function will be zero.

Given function is:

`R(p) = -10p^2+800p`

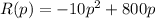
Taking derivative wrt p

`(d)/(dp) (R(p) = (d)/(dp) (-10p^2+800p)\\R'(p) = -10 (d)/(dp) (p^2) +800 \ frac{d}{dp}(p)\\R'(p) = -10 (2p) +800(1)\\R'(p) = -20p+800\\`

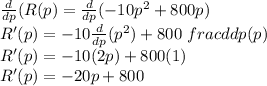
Now putting R'(p) = 0

`-20p+800 = 0\\-20p = -800\\(-20p)/(-20) = (-800)/(-20)\\p = 40`

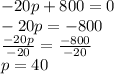
As p is is positive and the second derivative is -20, the function will have maximum value at p = 40

Putting p=40 in function

`R(40) = -10(40)^2 +800(40)\\= -10(1600) + 32000\\=-16000+32000\\=16000`

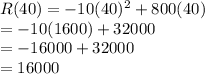
The maximum revenue is 16000 dollars (at p = 40)