Question

3x – 2y = 17
–2x – 5y = 14
Solve using Elimination Please show work

Answer 1

The solution is x=3 , y=-4 or (3,-4)

Explanation:

Given equations (1 and 2) are:

`3x- 2y = 17\\-2x -5y = 14`

To solve a system of equation with elimination method, the co-efficients of one of the variables has to be equated and then the equations are added or subtracted to get an equation in one variable.

Multiplying equation 1 by 2:

`2(3x-2y) = 2*17\\6x-4y = 34\ \ \ \ \ Eqn\ 3`

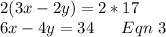
Multiplying equation 2 by 3

`3(-2x-5y) = 3*14\\-6x-15y = 42\ \ \ \ Eqn\ 4`

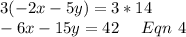
Adding equation 3 and 4

`(6x-4y) + (-6x-15y) = 34+42\\6x-4y-6x-15y = 76\\-19y = 76\\(-19y)/(-19) = (76)/(-19)\\y = -4\\`

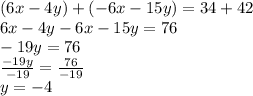
Putting y = -4 in equation 1

`3x-2(-4) = 17\\3x+8 = 17\\3x = 17-8\\3x = 9\\(3x)/(3) = (9)/(3)\\x = 3`

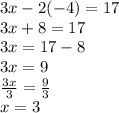
Hence,

The solution is x=3 , y=-4 or (3,-4)