Question

Find the circumference of the given circle

Answer 1

40.21

Explanation:

The circumference of a circle is 2πr; where are is the radius. The radius is not given but two points

(x1,y1) = (-2,2)

(x2,y2) = (3,-2)

With the two points you can use the distance formula which will be equal to the radius

r =
`\sqrt{(y2-y1)^(2) + (x2-x1)^(2) }`

r =
`\sqrt{(-2-2)^(2) + (3+2)^(2) }`

r =
`\sqrt{(-4)^(2) + (5)^(2) }`

r =
`√(41 )` = 6.40

circumference = 2πr = 2π(6.40) = 40.21

Answer 2

`\huge\boxed{2\pi√(41)}`

Hey! Start by finding the radius. We will assume that point
`P` is the center point of the circle, so the radius is the distance between points
`P` and
`Q`.

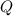Let's use the distance formula, substituting in the known values:

`\begin{aligned}r&=√((x_2-x_1)^2+(y_2-y_1)^2)\\&=√((-2-3)^2+(2-(-2))^2)\end{aligned}`

Simplify:

`\begin{aligned}r&=√((-2-3)^2+(2-(-2))^2)\\&=√((-5)^2+4^2)\\&=√(25+16)\\&=√(41)\end{aligned}`

Now, we'll use the formula for the circumference of a circle, substituting in the known value:

`\begin{aligned}C&=2\pi r\\&=\boxed{2\pi√(41)}\\&\approx40.232\end{aligned}`