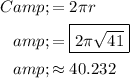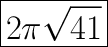
Hey! Start by finding the radius. We will assume that point
 is the center point of the circle, so the radius is the distance between points
is the center point of the circle, so the radius is the distance between points
 and
and
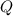 .
.
Let's use the distance formula, substituting in the known values:
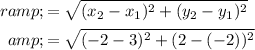
Simplify:
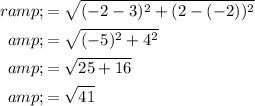
Now, we'll use the formula for the circumference of a circle, substituting in the known value: