Length of a rectangular sign :-
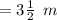
Width of a rectangular sign :-
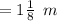
We know that :-
The formula for finding the area of a rectangle is :-
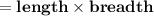
Which means :-
The area of the rectangular sign:-
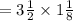

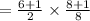
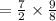
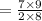
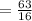
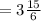
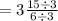
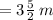
Thus, the area of the rectangular sign is:-
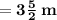
We can see that :-

Which will mean that the area of the rectangular sign is greater than
 .
.
Therefore, the area of the rectangular sign is =
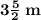 and it is greater than
and it is greater than
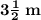 .
.