Answer:
Part A)
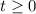
Part B)
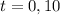
Part C)
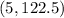
The firework reaches its maximum height of 122.5 meters after 5 seconds.
Explanation:
We are given the function of a firework's projectile:
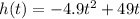
Where h(t) is the height after t seconds.
Part A)
The domain is our t.
In this case t is time.
Hence, a reasonable domain must be:
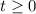
Time cannot be negative. Thus, our t must be greater than or equal to 0.
Part B)
To find the zeros of the function, we will set the equation equal to 0 and sole for t. Hence:
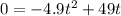
Divide everything by -4.9:
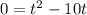
Factor:
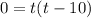
Zero Product Property:

Hence, our zeros are:
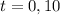
So, at t=0 and t=10 seconds the height h(t)=0.
Therefore, the zeros represent the times in which the firework is on the ground.
In this case, the first zero, t=0, tells us that the firework was originally on the ground before being projected (when no time has passed yet).
And the second zero, t=10, tells us that the firework lands after 10 seconds of its projection.
Part C)
Using Desmos, we can see that the vertex (turning point) is at (5, 122.5).
In this case, the vertex represents the maximum height our firework reaches.
Therefore, (5, 122.5) tells us that the firework reaches its maximum height at 122.5 meters after 5 seconds.