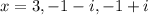Question

What are all the real and complex zeros of the polynomial function shown in the graph?​

Answer 1

`x=3, -1-i, -1+i`

Explanation:

We are given the graph of the function:

`f(x)=x^3-x^2-4x-6`

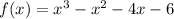
And we want to determine its real and complex roots.

First, notice that it crosses through the x-axis at 3. This means that (x-3) is a factor.

Hence, let's use synthetic division to factor. This yields:

3 | 1 -1 -4 -6

|_______(3)___(6)___(6)_________________

1 2 2 0

Therefore,this yields:

`f(x)=(x-3)(x^2+2x+2)`

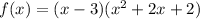
The right-most term is not factorable. Thus, we will need to use the quadratic formula.

Zero Product Property:

`0=x-3\text{ or } 0=x^2+2x+2`

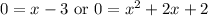
We will use the quadratic formula on the right. Our a=1, b=2, and c=2. Therefore:

`x=(-(2)\pm√((2)^2-4(1)(2)))/(2(1))`

Evaluate:

`x=(-2\pm√(-4))/(2)`

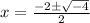
Simplify:

`x=(-2\pm2i)/(2)=-1\pm i`

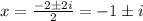
Hence, our solutions are:

`x=3, -1-i, -1+i`