Question

Juan is three times as old as Gabe and Gabe is six years older than Catherine. If the sum of their ages is 149, how old is each person? Define a variable, write an equation, solve the equation, and answer in a complete sentence.

Answer 1

Juan = 93 years.

Gabe = 31 years.

Catherine = 25 years.

Explanation:

Let the age of Juan = J

Let the age of Gabe = G

Let the age of Catherine = C

Translating the word problem into an algebraic equation, we have;

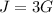`J = 3G` ..........equation 1

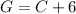`G = C + 6` ........equation 2

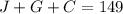`J + G + C = 149` ........equation 3

We would solve the linear equations by using the substitution method;

Substituting equation 2 into equation 1;

`J = 3(C + 6)`

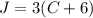
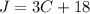`J = 3C + 18` ........equation 4

Substituting equation 2 and equation 4 into equation 3;

`(3C + 18) + (C + 6) + C = 149`

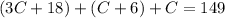
Simplifying the equation, we have;

`5C + 24 = 149`

`5C = 149 - 24`

`5C = 125`

`C = \frac {125}{5}`

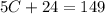
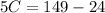
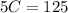
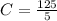
C = 25 years.

To find G; from equation 2

`G = C + 6`

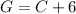
Substituting the value of "C" into equation 2, we have;

`G = 25 + 6`

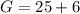
G = 31 years.

To find J; from equation 1

`J = 3G`

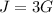
Substituting the value of "G" into equation 1, we have;

`J = 3 * 31`

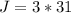
J = 93 years.

Therefore, Juan is 93 years old, Gabe is 31 years old and Catherine is 25 years old.