Question

A population of geese doubles every 18 months. If there are 5 geese initially, how many years will it take for there to be 111 geese?

Answer 1

Answer: 7 years

Explanation:

Let t be the number of periods in which geese doubles .

The exponential growth function:
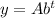`y=Ab^t` , where A = initial value , b= growth factor.

As per given , A = 5 , b=2

i.e. Number of geese after t periods =
`y=5(2)^t`

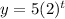
Put y=111, we get

`111=5(2)^t\\\\\Rightarrow\ (111)/(5)=2^t\\\\\Rightarrow\ 22.2=2^t`

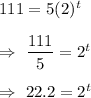
Taking log on both sides , we get

`\log 22.2 = t\log 2\\\\\Rightarrow\ 1.346353=t(0.30103)\\\\\Rightarrow\ t=(1.346353)/(0.30102)\\\\\Rightarrow\ t=4.47263636\approx4.47`

Now , total months = 4.47 x 18 =80.46≈ 80 months

since 1 year =12 months

Number of years it will take
`=(80)/(12)=(20)/(3)=6.66666666667\approx7`

Hence, it will take 7 years (approx.)