Question

In manufacturing processes, it is of interest to know with confidence the proportion of defective parts. Suppose that we want to be reasonably certain that less than 4% of a company’s widgets are defective. To test this, we obtain a random sample of 250 widgets from a large batch. Each of the 250 widgets is tested for defects, and 6 are determined to be defective, based upon the manufacturer’s standards. Using α = 0.01, is this evidence that less than 4% of the company’s widgets are defective? State the hypotheses, list and check the conditions, calculate the test statistic, find the p-value, and make a conclusion in a complete sentence related to the scenario.

Answer 1

The calculated value Z = 1.3114 < 2.576 at 0.01 level of significance

null hypothesis is accepted

The evidence that less than 4% of the company’s widgets are defective

Explanation:

Step(i):-

Given Population proportion

P = 4% = 0.04

Given sample proportion

`p = (6)/(250) = 0.024`

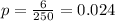
Null hypothesis :- P < 0.04

Alternative Hypothesis : P ≠ 0.04

Step(ii):-

Test statistic

`Z = \frac{p-P}{\sqrt{(PQ)/(n) } }`

`Z = \frac{0.024-0.04}{\sqrt{(0.04 X 0.96)/(250) } }`

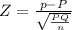
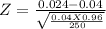
Z = - 1.3114

|Z| = | - 1.3114|

The tabulated value Z = 2.576

The calculated value Z = 1.3114 < 2.576 at 0.01 level of significance

null hypothesis is accepted

The evidence that less than 4% of the company’s widgets are defective