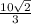Question

Determine the point of intersection of right bisectors in a triangle ∆ with vertices A (-3, 5), B (1, 1) and (−7, −3). Find the distance from the point of intersection to each vertex of the triangle.

Answer 1

Point of intersection (-11/3 , 1/3)

All distances from the vertices are
`(10√(2) )/(3)`

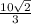
Explanation:

The vertices of the triangle is A(-3,5) , B (1,1) and C (-7,-3)

We need to find the perpendicular bisector of the triangle first

let's take one side connecting A and B

mid point of A and B = (-1,3)

Slope of the line joining A and B = -1

slope of perpendicular to line joining A and B = 1

equation of line passing through (-1,3) with slope 1

y - 3 = 1(x-(-1))

y -3 = x+1

x-y = -4 ............(1)

similarly

mid point joining B and C = (-3,-1)

slope perpendicular to line joining B and C = -2

Equation of perpendicular bisector of line joining B and C =

y +1 = -2(x +3 )

y+1 = -2x -6

2x+y = -7 ..........(2)

On solving 1 and 2

x= -11/3 , y= 1/3

Distances

From A =
`(10√(2) )/(3)`

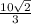
From B =
`(10√(2) )/(3)`

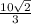
From C =
`(10√(2) )/(3)`