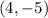Answer:
Given system of equations:
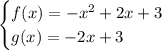
To solve by substitution, equate the equations and solve for x:
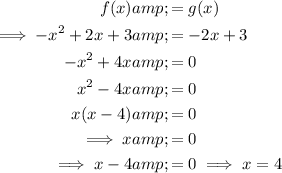
Therefore, the x-values of the solution are
 and
and
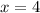 .
.
To find the y-values of the solution, substitute the found values of x into the functions:
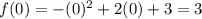
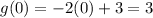
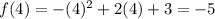
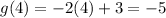
Therefore, the solutions to the given system of equations are:
 and
and