Question

5. Select ALL of the following expressions that are linear functions (they do not need to be in slope-intercept form).

y2 = 5x +2
2x + 4 = 3x - 8
y = 3x - 2
y + x2 = 12
y = x2 + 2x
1
3x + -y = 24

Answer 1

The following are the LINEAR functions.

• 
  `2x\:+\:4\:=\:3x\:-\:8`

• 
  `y = 3x - 2`

• 
  `1`

• 
  `3x\:+\:-y\:=\:24`

Explanation:

We know that linear functions are the equations with a straight line graph in an XY plane.

Also, a linear function is a function of the form

`f(x)=mx+b`

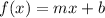
where m is the slope and b is the y-intercept. The only power of the variable is 1.

So, from the given expressions we can determine that:

1)
`y^2=\:5x\:+2`

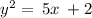
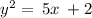`y^2=\:5x\:+2` is NOT a linear function because the power of y is 2, hence the graph won't be a straight line. Therefore, it is not a linear function

2)
`2x\:+\:4\:=\:3x\:-\:8`

`2x\:+\:4\:=\:3x\:-\:8`

`x=12`

This is a linear equation is an equation of a straight line, written in one variable. The only power of the variable is 1

3)
`y = 3x - 2`

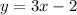
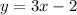`y = 3x - 2` is a linear function because it is of the form
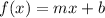`f(x)=mx+b` and the power of its x and y variables is 1. Hence, the function has a straight line graph.

4)
`y\:+\:x^2\:=\:12`

`y\:+\:x^2\:=\:12` is NOT a linear function because the power of x is 2, hence the graph won't be a straight line. Therefore, it is not a linear function.

5)
`y\:=\:x^2\:+\:2x`

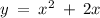
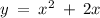`y\:=\:x^2\:+\:2x` is NOT a linear function because the power of x is 2, hence the graph won't be a straight line. Therefore, it is not a linear function.

6)
`1`

`1` is a constant function and a constant function is also considered linear in this context, as it is a polynomial of degree
`0` or is the
`0` polynomial.

7)
`3x\:+\:-y\:=\:24`

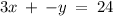
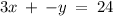`3x\:+\:-y\:=\:24` is a linear function as the power of its x and y variables is 1. Hence, the function has a straight line graph. Therefore, it is a linear function.

In a summary, the following are the LINEAR functions.

• 
  `2x\:+\:4\:=\:3x\:-\:8`

• 
  `y = 3x - 2`

• 
  `1`

• 
  `3x\:+\:-y\:=\:24`