Question

At 9 AM there are 37 bacteria in a dish and they start doubling every 15 minutes. At t = 274 minutes an

antibacterial organism is introduced into the dish which stops its growth and begins destroying 6% of it every
24 minutes. How many bacteria are in the dish at 7 PM? Round your answer to the nearest whole number.

Answer 1

5,035,041

Explanation:

Exponential growth:

`y = a(1 + r)^(x)`

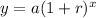
y = future amount

a = initial amount

r = growth rate

x = number of periods

Part A: growth at the rate of doubling each 15 minutes for 274 minutes

Each period is 15 minutes.

a = 37

x = 274/15 = number of periods

r = 100%

`y = 37(1 + 1)^{(274)/(15)`

-------------------------------------------------------------------------------------

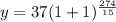
Exponential decay:

`y = a(1 - r)^(x)`

The growth takes place from 9 AM for 274 minutes, or 4 hours and 34 minutes, until 1:34 PM. The decay goes from 1:34 PM to 7 PM, or 5 hours and 26 minutes, or 326 minutes

Part B: decay at the rate of 6% each 24 minutes for 326 minutes

`y = 37(1 + 1)^{(274)/(15)}(1 - 0.06)^{(326)/(24)}`

`y = 5035041`

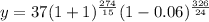
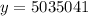
Answer: 5,035,041