Solve the following compound inequality. A. B. C. D.

Question

asked Nov 6, 2021 529 views

2 Answers

Berserkk · Answer 1 · 2021-11-07T18:19:12+0000

Answer:

C

Explanation:

We have the compound inequality:

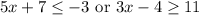
$5x+7\leq-3\text{ or } 3x-4\geq11$

We will solve each inequality individually and then combine them at the end.

For the first inequality, we have:

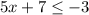
$5x+7\leq-3$

Subtract 7 from both sides:

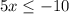
$5x\leq-10$

Divide both sides by 5:

$x\leq-2$

For the second inequality, we have:

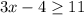
$3x-4\geq11$

Add 4 to both sides:

$3x\geq15$

Divide both sides by 3:

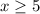
$x\geq5$

Since our original inequality was an “OR,” our solution set is also an “OR.”

Hence, our solution is:

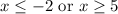
$x\leq-2\text{ or } x\geq5$

Thus, our answer is C.