
To solve for
 , we need to isolate it on one side of the equation.
, we need to isolate it on one side of the equation.
Take the square root of both sides, making sure to use both positive and negative roots.
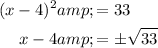
 cannot be simplified, so we'll leave it as-is.
cannot be simplified, so we'll leave it as-is.
Add
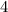 to both sides to fully isolate
to both sides to fully isolate
 .
.

Expand the solution by making two solutions, one where
 is positive and one where it's negative.
is positive and one where it's negative.
