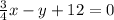Question

A line passes through the point (-8,6) and has a slope of 3/4 in general form

Answer 1

y = 3/4x + 12

Explanation:

let equation of the line be y = 3/4x + b

sub (-8, 6):

6 = 3/4(-8) + b

12 = b

therefore equation of the line is y = 3/4x + 12

Topic: Coordinate Geometry

If you would like to venture further, you can check out my Instagram page (learntionary) where I post notes and mathematics tips. Thanks!

Answer 2

General Form of Equation of a line that passes through the point (-8,6) and has a slope of 3/4 is:

`(3)/(4)x-y+12=0`

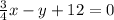
Explanation:

We need to find equation of line that passes through the point (-8,6) and has a slope of 3/4 in general form.

The general form of linear equation is
`Ax+By+C=0`

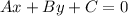
First we will use slope-intercept form i.e,
`y=mx+b` to find equation and then write it in general form.

Where m is slope and b is y-intercept.

We are given slope = 3/4 but y-intercept is not given and we need to find.

Finding y-intercept

Using the point (-8,6) and slope m = 3/4 we can find y-intercept

`y=mx+b\\6=(3)/(4)(-8)+b\\6=3(-2)+b\\6=-6+b\\b=6+6\\b=12`

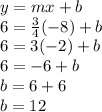
So, y-intercept b is 12

Equation of line

The line has slope m=3/4 and y-intercept b is 12, the equation is:

`y=mx+b\\y=(3)/(4)x+12`

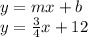
General Form of Equation of a line that passes through the point (-8,6) and has a slope of 3/4 is:

`(3)/(4)x-y+12=0`