Question

Mrs. Culland is finding the center of a circle whose equation

is x2 + y2 + 6x - 4y – 3 = 0 by completing the square. Her
work is shown.
x2 + y2 + 6x + 4y - 3 = 0
x2 + 6x + y2 + 4y - 3 = 0
(x2 + 6x) + (12 + 4y) = 3
(x2 + 6x + 9) + (y2 + 4y + 4) = 3 + 9 + 4
Which completes the work correctly?
(x - 3)2 + ( - 2)= 42, so the center is (3,2).
(x + 3)2 + (y + 2)2 = 42, so the center is (3, 2).
(x - 3)2 + (x - 2)2 = 42, so the center is (-3,-2).
(x + 3)2 + (y + 2)2 = 42, so the center is (-3, -2).

Answer 1

D,,,, (x+3)²+(y+2)²=4², so the center is (-3, -2).

Explanation:

Answer 2

centre of circle (h,k) is (-3,-2)

Option D is Correct.

Explanation:

The centre of circle can be found from the equation as:

`(x-h)^2+(y-k)^2=r^2 \ then \ (h,k) \ is \ center`

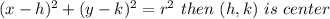
So, the steps then by Mrs Culland are:

`x^2 + y^2 + 6x + 4y - 3 = 0\\x^2 + 6x + y^2 + 4y - 3 = 0\\(x^2 + 6x) + (y^2 + 4y) = 3\\(x^2 + 6x + 9) + (y^2 + 4y + 4) = 3 + 9 + 4`

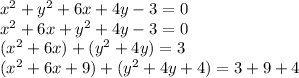
The next step will be:

`(x + 3)^2 + (y + 2)^2 = 16`

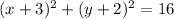
I assume there is some calculating mistake in the given options. Instead of 42 there should be 16, according to solution shown above.

The general equation of circle is

`(x-h)^2+(y-k)^2=r^2 \ then \ (h,k) \ is \ center`

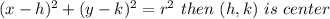
In our case:
`(x + 3)^2 + (y + 2)^2 = 16`

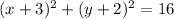
h= -3 and k= -2, so the centre of circle (h,k) is (-3,-2)

Option D is Correct.