Answer:
We conclude that the sequence is NEITHER geometrc nor arithmetic.
Explanation:
Given the sequence
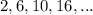
As we know that
An arithmetic sequence has a constant difference d and is defined by:
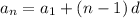
Computing the differences between all adjacent terms:
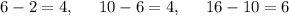
The difference is not constant
Hence, the sequence is NOT arithmetic.
NOW, let's check whether is a geometric sequence or not
A geometric sequece has a constant common ration r and is defined by:
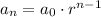
Computing the common ratios between all adjacent terms:
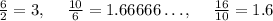
The ratio is not constant
Hence, the sequence is NOT geometric.
Therefore, we conclude that the sequence is NEITHER geometrc nor arithmetic.