Question

Given C(x, 16), D(2,-4), E(-6 4), and F(-2, 4) find the value of x so that line CD is parellel to lin EF. please show work

Answer 1

The value of x = -6

Explanation:

We know that if the line CD is parallel to line EF, then their slopes will be the same.

In other words:

slope
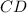`CD` = slope
`EF`

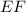
As we know that the slope between two points will be:

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

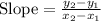
Let's find the slope of CD

as

• C(x, 16)

• D(2,-4)

`m\:\left(CD\right)=(-4-16)/(2-x)`

`=-(20)/(2-x)`

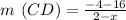
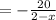
Now, let's find the slope of EF

as

• E(-6, 14)

• F(-2, 4)

`m\left(EF\right)=(4-14)/(-2-\left(-6\right))`

`=-(10)/(4)`

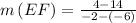
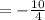
As we already pointed out that

`m\left(CD\right)=\:m\left(EF\right)`

`-(20)/(2-x)`
`=-(10)/(4)`

`-20\cdot \:4=-\left(2-x\right)\cdot \:10`

`(-\left(2-x\right)\cdot \:10)/(-10)=(-80)/(-10)`

`2-x=8`

`x=-6`

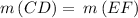
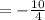
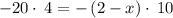
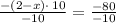
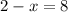
Therefore, the value of x = -6