Question

A yo‑yo with a mass of 0.0800 kg and a rolling radius of =2.70 cm rolls down a string with a linear acceleration of 5.70 m/s2.

Calculate the tension magnitude in the string and the angular acceleration magnitude of the yo‑yo. What is the moment of inertia of this yo‑yo?

I ended up calculating the angular acceleration to be 211.11 but I'm unsure how to calculate the other parts of the problem.

Answer 1

Step-by-step explanation:

Given that,

Mass, m = 0.08 kg

Radius of the path, r = 2.7 cm = 0.027 m

The linear acceleration of a yo-yo, a = 5.7 m/s²

We need to find the tension magnitude in the string and the angular acceleration magnitude of the yo‑yo.

(a) Tension :

The net force acting on the string is :

ma=mg-T

T=m(g-a)

Putting all the values,

T = 0.08(9.8-5.7)

= 0.328 N

(b) Angular acceleration,

The relation between the angular and linear acceleration is given by :

`\alpha =(a)/(r)\\\\\alpha =(5.7)/(0.027)\\\\=211.12\ m/s^2`

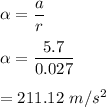
(c) Moment of inertia :

The net torque acting on it is,
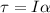`\tau=I\alpha`, I is the moment of inertia

Also,
`\tau=Fr`

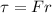
So,

`I\alpha =Fr\\\\I=(Fr)/(\alpha )\\\\I=(0.328* 0.027)/(211.12)\\\\=4.19* 10^(-5)\ kg-m^2`

Hence, this is the required solution.