Answer:
The object takes approximately 1.180 seconds to complete one horizontal circle.
Step-by-step explanation:
From statement we know that the object is experimenting an Uniform Circular Motion, in which acceleration (
 ), measured in meters per square second, is entirely centripetal and is expressed as:
), measured in meters per square second, is entirely centripetal and is expressed as:
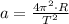 (1)
(1)
Where:
 - Period of rotation, measured in seconds.
- Period of rotation, measured in seconds.
 - Radius of rotation, measured in meters.
- Radius of rotation, measured in meters.
If we know that
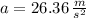 and
and
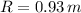 , then the time taken by the object to complete one revolution is:
, then the time taken by the object to complete one revolution is:
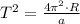
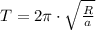
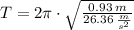
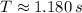
The object takes approximately 1.180 seconds to complete one horizontal circle.