Question

The Key Club is having a fundraising dinner for charity. The venue that holds a maximum of 500 people will

cost $1000 and it costs $20 per person for the food. The two charity representatives get to attend for free.
Write an inequality and then determine how many people must come to keep costs at most $25 per person.

Answer 1

`(\$1000+\$20x)/(x) \leq \$25`

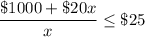
Minimum 200 people other than the 2 charity representatives.

Explanation:

Given that:

The venue can hold a maximum of 500 people.

Cost of venue = $1000

Per person cost for food = $20

Two charity representatives get to attend the dinner for free.

To find:

The inequality and to determine how many people must come to keep costs at most $25.

Solution:

Let the number of people attending the dinner =
`x`

Cost of food for
`x` people =
`\$20x`

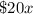
Total cost = $1000 +
`\$20x`

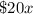
Cost per person = Total cost divided by Number of people attending the dinner.

As per question statement:

`(\$1000+\$20x)/(x) \leq \$25\\\Rightarrow 1000+20x\leq25x\\\Rightarrow 1000 \leq 5x\\\Rightarrow x\geq 200`

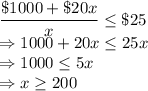
Therefore, the answer is:

Minimum 200 people other than the 2 charity representatives should attend the dinner.