Final answer:
To find the probabilities, the binomial probability formula is used, where for (a) we calculate for exactly 3 adults, for (b) we calculate the complement of having at most 3 adults, and for (c) we sum the probabilities of having 0, 1, or 2 adults choosing cashews as their favorite nut.
Step-by-step explanation:
To solve this probability question, we will use the binomial probability formula which is given by:
P(X = k) = (n choose k) *
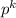 *
*
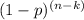
where:
- n is the number of trials (in this case, 12 adults)
- k is the number of successes (number of adults choosing cashews as their favorite nut)
- p is the probability of success on an individual trial (39%), or 0.39
Part (a): Exactly Three
P(X = 3) = (12 choose 3) *
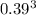 *
*
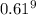
Part (b): At Least Four
P(X ≥ 4) = 1 - P(X ≤ 3), which is 1 minus the sum of the probabilities of having 0, 1, 2, or 3 adults choosing cashews.
Part (c): At Most Two
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)